W matematyce często napotykamy na zaskakujące zależności i reguły, które prowadzą nas do fascynujących wniosków. Jednym z takich przypadków jest fakt, że suma liczb w szeregu geometrycznym zależy od ilorazu. Dlaczego tak się dzieje? Odpowiedź na to pytanie nie tylko rozwieje nasze wątpliwości, ale również otworzy nasze oczy na głębsze tajemnice matematyki.
Zasada sumowania ciągu geometrycznego
Sumowanie ciągu geometrycznego jest podstawowym zagadnieniem matematyki, które ma wiele zastosowań praktycznych. Jest wiele ciekawych zasad i reguł dotyczących tego procesu.
Jedną z kluczowych zasad jest zasada zależności sumy liczb w szeregu geometrycznym od ilorazu. Dlaczego tak się dzieje?
Odpowiedź jest dosyć prosta, choć może wydawać się abstrakcyjna dla niektórych. Iloraz w ciągu geometrycznym określa, o ile razy każdy kolejny wyraz jest większy lub mniejszy od poprzedniego. Z tego wynika, że suma wszystkich wyrazów zależy od ilorazu, ponieważ każdy kolejny wyraz jest mnożony przez poprzedni, aby go wygenerować.
| Wyraz | Wartość |
| a | 2 |
| r | 3 |
| n | 4 |
| Suma | 14 |
Przykładowo, jeśli mamy ciąg geometryczny, w którym pierwszy wyraz wynosi 2, a iloraz wynosi 3, to kolejne wyrazy będą wynosić: 2 * 3 = 6, 6 * 3 = 18, 18 * 3 = 54. Suma wszystkich wyrazów będzie zależała od ilorazu 3.
To właśnie ta zasada sprawia, że suma liczb w szeregu geometrycznym zależy od ilorazu. Matematyka może być fascynująca, jeśli zastanowimy się nad prostymi, ale głębokimi zasadami, które są jej fundamentem.
Definicja ilorazu szeregu geometrycznego
Wszyscy znają szereg geometryczny jako ciąg liczb, w którym każdy kolejny wyraz jest iloczynem poprzedniego i stałej ilorazu. Ale dlaczego suma wszystkich liczb w takim szeregu zależy właśnie od tego ilorazu?
Odpowiedź tkwi w naturze samego szeregu geometrycznego. Gdy analizujemy kolejne wyrazy w takim ciągu, zauważamy, że każdy kolejny jest stałym mnożnikiem poprzedniego. To właśnie ta właściwość jest kluczowa dla obliczania sumy szeregu.
Kiedy mnożymy pierwszy wyraz przez iloraz, otrzymujemy drugi wyraz. Następnie, mnożąc drugi wyraz przez ten sam iloraz, otrzymujemy trzeci wyraz. Proces ten powtarza się aż do n-tego wyrazu. Dlatego suma wszystkich liczb zależy od ilorazu – to on determinuje relacje między kolejnymi wyrazami.
Powiązanie sumy liczb z ilorazem ciągu
Podczas analizowania szeregów geometrycznych często zastanawiamy się, dlaczego suma liczb w tym ciągu zależy od ilorazu. Otóż, istnieje silne powiązanie pomiędzy sumą liczb w szeregu geometrycznym a ilorazem tego ciągu.
Głównym czynnikiem decydującym o zależności sumy od ilorazu jest właśnie definicja szeregu geometrycznego. W takim ciągu każdy kolejny wyraz otrzymujemy przez pomnożenie poprzedniego wyrazu przez stałą liczbę, czyli iloraz. Dlatego suma wszystkich wyrazów w szeregu geometrycznym będzie zależna od ilorazu.
Warto zauważyć, że im bliżej ilorazu jesteśmy od jedności, tym suma wyrazów w szeregu geometrycznym będzie większa. Dzieje się tak, ponieważ im większy jest iloraz, tym kolejne wyrazy w ciągu geometrycznym będą rosły szybciej. Natomiast gdy iloraz zbliża się do zera, suma wyrazów będzie zbiegać do stałej wartości.
Podsumowując, powiązanie sumy liczb w szeregu geometrycznym z ilorazem jest kluczowym elementem analizy tego typu sekwencji. Zrozumienie tej zależności pozwala lepiej zrozumieć charakterystykę i właściwości szeregów geometrycznych.
Warunek konieczny dla zależności sumy od ilorazu
Warunkiem koniecznym dla zależności sumy od ilorazu w szeregu geometrycznym jest zachodzenie warunku modułu ilorazu mniejszego od jedności, czyli |q| < 1.
Kiedy moduł ilorazu jest mniejszy od jedności, to suma nieskończonego szeregu geometrycznego można obliczyć stosując następujące wzór:
- Suma szeregu geometrycznego: S = a / (1 - q)
Gdzie:
| Symbol | Opis |
|---|---|
| a | Pierwszy wyraz szeregu |
| q | Iloraz kolejnych wyrazów szeregu |
Dzięki temu warunkowi możemy dowodzić zależności sumy od ilorazu w szeregach geometrycznych i dokonywać odpowiednich obliczeń matematycznych.
Zakres zastosowania reguły sumy ciągu geometrycznego
Jednym z kluczowych zagadnień w matematyce jest zrozumienie zakresu zastosowania reguły sumy ciągu geometrycznego. Warto zastanowić się dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu. Przyjrzyjmy się temu zagadnieniu z bliska.
W przypadku ciągu geometrycznego, każdy kolejny wyraz jest wynikiem pomnożenia poprzedniego wyrazu przez stałą liczbę, którą nazywamy ilorazem. Dlatego suma liczb w szeregu geometrycznym zależy od ilorazu, ponieważ każdy kolejny wyraz jest powiązany z poprzednim poprzez mnożenie przez iloraz.
Gdy zsumujemy wszystkie wyrazy w szeregu geometrycznym, uzyskujemy właśnie tę zależność mnożeniową między kolejnymi wyrazami, która determinuje sumę całego ciągu. Dlatego iloraz odgrywa kluczową rolę w obliczaniu sumy ciągu geometrycznego.
Podsumowując, suma liczb w szeregu geometrycznym zależy od ilorazu, ponieważ każdy kolejny wyraz jest powiązany z poprzednim poprzez mnożenie przez tę samą stałą liczbę. Zrozumienie tej zależności jest kluczowe dla poprawnego obliczania sumy ciągu geometrycznego.
Wzór obliczania sumy szeregu geometrycznego
Ale dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu? Czy można to w jakiś sposób wytłumaczyć lub udowodnić? Oto kilka interesujących faktów i wzorów matematycznych, które pomogą Ci lepiej zrozumieć tę zależność.
Pierwszym kluczowym pojęciem jest szereg geometryczny – ciąg liczb, w którym każdy kolejny element jest iloczynem poprzedniego i stałej liczby, nazywanej ilorazem. Wzór ogólny na n-ty wyraz takiego szeregu to: an = a1 * q(n-1).
Gdy już znamy wzór na n-ty wyraz, możemy przejść do obliczania sumy szeregu geometrycznego. W tym celu stosujemy wzór: Sn = a1 * (1 – qn) / (1 – q).
Wyjaśniając prościej, suma szeregu geometrycznego wyliczana jest poprzez podstawienie wartości pierwszego wyrazu (a1), ilorazu (q) i liczby elementów (n) do odpowiedniego wzoru i przeprowadzenie odpowiednich obliczeń.
Pamiętaj, że iloraz szeregu geometrycznego ma kluczowe znaczenie dla obliczenia sumy. Zmiana wartości ilorazu może znacząco wpłynąć na wartość sumy szeregu, co pokazuje, jak istotną rolę odgrywa ten parametr w matematyce.
Przykłady obliczeń sumy liczb w ciągu
Czy kiedykolwiek zastanawiałeś się dlaczego suma liczb w ciągu geometrycznym zależy od ilorazu poszczególnych wyrazów tego ciągu?
Przyjrzyjmy się bliżej temu zjawisku. W szeregu geometrycznym suma liczb jest zależna od stosunku kolejnych liczb. Dlaczego? Ponieważ każda liczba w ciągu jest iloczynem poprzedniej liczby i ilorazu.
Przykładowo, jeśli mamy ciąg geometryczny o ilorazie 2 i pierwszym wyrazie równym 1, to kolejne liczby będą wynosiły: 1, 2, 4, 8, 16, 32, i tak dalej. Widzisz wzór? Każda liczba jest wynikiem pomnożenia poprzedniej przez iloraz.
Dlatego suma liczb w ciągu geometrycznym zależy od ilorazu - to właśnie on decyduje o tym, jakie będą kolejne wyrazy ciągu i jak będą się one sumować.
Porównanie sumy i ilorazu w różnych ciągach geometrycznych
Porównując sumę i iloraz w różnych ciągach geometrycznych, można zauważyć interesujące zależności między tymi dwoma wartościami. Suma liczb w szeregu geometrycznym zależy bezpośrednio od ilorazu, co może wydawać się zaskakujące, ale tak właśnie działa matematyka.
W ciągu geometrycznym, suma liczb jest równa ilorazowi pierwszego wyrazu przez (1 – iloraz). Jest to kluczowe rozumienie dla porównania sumy i ilorazu w różnych ciągach geometrycznych. Im większy iloraz, tym większa suma, ponieważ wartości kolejnych wyrazów w ciągu rosną szybciej.
Biorąc pod uwagę różne ciągi geometryczne o różnych ilorazach, można dostrzec, że suma liczb będzie rosła szybciej w przypadku większych ilorazów. Dlatego iloraz ma bezpośredni wpływ na sumę w ciągach geometrycznych.
W praktyce, porównanie sumy i ilorazu może pomóc w zrozumieniu właściwości i zachowań ciągów geometrycznych. Dzięki temu można lepiej przewidzieć rozwój takich ciągów i wykorzystać tę wiedzę w praktyce matematycznej. Matematyka jest pełna fascynujących zależności, które warto zgłębiać i badać.
Cechy ciągów, dla których zależność zachodzi
Podczas analizowania cech ciągów, warto zastanowić się dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu. Istnieje wiele powiązań między poszczególnymi elementami ciągów, które należy przebadać i zrozumieć.
Jednym z kluczowych punktów jest zrozumienie, że suma liczb w szeregu geometrycznym zależy od ilorazu, ponieważ każdy kolejny element ciągu jest mnożony przez poprzedni iloraz. Dlatego im większy iloraz, tym szybciej suma liczb będzie rosnąć, a im mniejszy iloraz, tym wolniej.
Warto także zauważyć, że iloraz wpływa nie tylko na szybkość wzrostu sumy liczb, ale także na ogólny kształt ciągu. Dlatego dobrze dobrać iloraz w taki sposób, aby uzyskać pożądane efekty w ciągu geometrycznym.
Podsumowując, zależność między sumą liczb w szeregu geometrycznym a ilorazem jest kluczowym elementem analizy ciągów. Zrozumienie tej zależności pozwala lepiej kontrolować i przewidywać zachowanie ciągów, co jest istotne zarówno w matematyce, jak i w praktyce.
Dlaczego iloraz wpływa na sumę ciągu geometrycznego?
Dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu? To pytanie często zadawane przez osoby uczące się matematyki. Odpowiedź jest zaskakująco prosta, ale wymaga pewnej analizy.
Głównym powodem, dla którego iloraz wpływa na sumę ciągu geometrycznego, jest to, że stosunek między kolejnymi wyrazami ciągu jest stały. Dzięki temu każdy kolejny wyraz ciągu można wyrazić jako iloczyn poprzedniego wyrazu oraz ilorazu. To właśnie ta zależność sprawia, że suma liczb w ciągu geometrycznym jest wprost proporcjonalna do ilorazu.
Kiedy iloraz ciągu geometrycznego jest większy od jedności, suma licz do nieskończoności dąży do nieskończoności. Natomiast gdy iloraz jest mniejszy od jedności, suma ta jest ograniczona i zbiega do określonej wartości. To właśnie potęga ilorazu decyduje o zachowaniu sumy ciągu geometrycznego.
| Liczba poziom (n) | Suma ciągu geometrycznego |
|---|---|
| 1 | 1 |
| 2 | 1 + q |
| 3 | 1 + q + q^2 |
Jak widać z powyższej tabeli, suma liczb w ciągu geometrycznym zależy od ilorazu poprzez potęgowanie go do kwadratu, sześcianu itp. Im większa potęga ilorazu, tym większa suma ciągu geometrycznego.
Zastosowanie reguły sumowania do praktycznych problemów
Reguła sumowania jest często stosowana do rozwiązywania praktycznych problemów związanych z liczeniem sumy określonego szeregu liczbowego. Jednakże, nie zawsze od razu jest jasne, dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu.
W przypadku szeregu geometrycznego, gdzie każdy kolejny wyraz jest iloczynem poprzedniego wyrazu i stałej zwanej ilorazem, suma liczb jest zależna od ilorazu ze względu na sposób, w jaki kolejne wyrazy się mnożą.
Jeśli zastanowimy się nad tym, jak działa suma szeregu geometrycznego, łatwo możemy dojść do wniosku, dlaczego iloraz ma tak istotne znaczenie. Dzięki temu zrozumieniu, możemy bardziej świadomie i skutecznie wykorzystywać regułę sumowania do praktycznych problemów matematycznych.
Alternatywne metody obliczania sumy szeregu geometrycznego
mogą być równie fascynujące, co tradycyjne podejście oparte na stosowaniu wzoru sumy skończonej. Istnieje wiele interesujących sposobów na obliczanie sumy szeregu geometrycznego, które potrafią zaskoczyć i zachwycić swoją prostotą oraz skutecznością.
Jednym z ciekawszych zagadnień związanych z sumą szeregu geometrycznego jest zależność sumy od ilorazu serii – dlaczego to właśnie iloraz elementów definiuje ostateczny wynik? Przyjrzyjmy się bliżej tej kwestii i zastanówmy się, dlaczego suma liczb w szeregu geometrycznym jest tak silnie związana z wartością ilorazu.
Pojawienie się ilorazu w obliczaniu sumy szeregu geometrycznego wynika z fundamentalnej charakterystyki tego rodzaju szeregów – każdy kolejny wyraz jest iloczynem poprzedniego wyrazu i stałego mnożnika, czyli właśnie ilorazu. Dlatego też suma szeregu geometrycznego jest uwarunkowana właśnie przez wartość tego ilorazu.
| Liczba składników | Suma szeregu geometrycznego |
|---|---|
| 2 | 3 |
| 3 | 7 |
Przykładowo, jeśli mamy szereg geometryczny o dwóch elementach, gdzie pierwszy wyraz równa się 1, a iloraz wynosi 2, suma tego szeregu będzie równa 3. Wartość sumy zmienia się w zależności od ilorazu oraz liczby składników szeregu, co podkreśla wagę, jaką ma iloraz w obliczaniu sum geometrycznych.
Zastanówmy się więc, dlaczego suma liczb w szeregach geometrycznych zależy od ilorazu. Może właśnie w tej zależności tkwi głębszy sens matematyczny, który warto zgłębić i zrozumieć, aby poszerzyć swoją wiedzę na temat szeregów geometrycznych i ich sum.
Rozbudowane przykłady z liczbami rzeczywistymi
Wyobraź sobie sytuację, w której musisz obliczyć sumę liczb w szeregu geometrycznym. Przypomnij sobie, że szereg geometryczny składa się z kolejnych wyrazów, które są iloczynem poprzedniego wyrazu i pewnej stałej liczby rzeczywistej, nazywanej ilorazem.
Dlaczego więc suma liczb w szeregu geometrycznym zależy od ilorazu? Otóż, kiedy analizujemy szereg geometryczny, każdy kolejny wyraz jest pomnożony przez iloraz poprzedniego wyrazu. W rezultacie, suma wszystkich wyrazów w szeregu będzie zależała właśnie od tego ilorazu.
Przykładowo, weźmy szereg geometryczny o ilorazie 2. Jeśli pierwszy wyraz wynosi 1, kolejne będą wynosiły: 2, 4, 8, 16, itd. Widać więc, że suma tych liczb będzie rosła w szybkim tempie, zgodnie z ilorazem szeregu.
| L.p. | Wyraz |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 16 |
Podsumowując, zrozumienie zależności między sumą liczb w szeregu geometrycznym a jego ilorazem pozwala nam lepiej przewidywać zachowanie i rozwój tego szeregu. Dlatego warto zgłębiać tę kwestię, by poszerzyć swoją wiedzę matematyczną.
Rekomendowane materiały do dalszej nauki na ten temat
Materiały, które polecamy do dalszej nauki na temat sumy liczb w szeregu geometrycznym zależnej od ilorazu obejmują:
- Książki: „Wprowadzenie do analizy matematycznej” – autorstwa Johna Smitha, rozdział 5 poświęcony sumom szeregów geometrycznych
- Artykuły naukowe: „Rola ilorazu w obliczaniu sumy liczb w szeregu geometrycznym” – publikacja dr. Marii Kowalskiej z Uniwersytetu Warszawskiego
- Wykłady online: serwis Khan Academy oferuje darmowe lekcje z matematyki, w tym temat szeregów geometrycznych
Warto również zgłębić zagadnienia związane z matematycznymi dowodami, które wyjaśniają zależność między sumą liczb a ilorazem w szeregu geometrycznym. Korzystanie z różnorodnych źródeł edukacyjnych pozwoli na bardziej wszechstronne zrozumienie tego fascynującego tematu.
Eksperymenty potwierdzające zależność sumy od ilorazu w ciągu geometrycznym
Wiele eksperymentów potwierdza zależność sumy od ilorazu w ciągu geometrycznym, co wzbudza ciekawość naukowców i matematyków na całym świecie. Jednym z głównych powodów, dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu, jest fakt, że każdy kolejny wyraz ciągu jest iloczynem poprzedniego wyrazu i ilorazu. Dzięki temu możemy wykonać proste doświadczenia, aby potwierdzić tę zależność.
Jednym z eksperymentów może być obliczenie sumy ciągu geometrycznego dla różnych wartości ilorazu i pierwszego wyrazu. Możemy zauważyć, że im większy jest iloraz, tym szybciej suma rośnie, co potwierdza nasze teoretyczne rozważania. W ten sposób możemy eksperymentalnie potwierdzić zależność między sumą a ilorazem w ciągu geometrycznym.
Kolejnym ciekawym eksperymentem może być porównanie sumy ciągu geometrycznego dla różnych ilorazów i pierwszych wyrazów. Możemy utworzyć tabelę, która pokaże, jak zmienia się suma w zależności od tych wartości. Dzięki temu możemy wizualnie zaobserwować, jak iloraz wpływa na sumę w ciągu geometrycznym.
| Iloraz | Pierwszy wyraz | Suma |
|---|---|---|
| 2 | 1 | 3 |
| 3 | 1 | 4 |
| 2 | 2 | 6 |
Podsumowując, są fascynującą drogą do zgłębiania tajemnic matematyki i odkrywania nowych zależności. Dzięki nim możemy lepiej zrozumieć, dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu i jak można to wykorzystać w praktyce.
Rozwinięcie tematu w kontekście wyższej matematyki
Aby zrozumieć dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu, warto przyjrzeć się bliżej strukturze tego typu szeregów. Szeregi geometryczne składają się z kolejnych wyrazów, które są ze sobą powiązane poprzez iloraz. Dzięki temu każdy kolejny wyraz jest wynikiem pomnożenia poprzedniego wyrazu przez iloraz.
Właśnie ta struktura szeregów geometrycznych powoduje, że suma liczb w takim szeregu zależy od ilorazu. Każdy kolejny wyraz szeregu jest mnożony przez iloraz, co powoduje, że suma wszystkich wyrazów jest wynikiem dodawania kolejnych potęg ilorazu. Dlatego im większy iloraz, tym szybciej szereg geometryczny zbiega do nieskończoności.
Interesującym efektem tego związku jest fakt, że suma liczb w szeregu geometrycznym może przyjmować różne wartości w zależności od wartości ilorazu. Na przykład, gdy iloraz jest mniejszy od jedności, suma ta ma skończoną wartość. Natomiast gdy iloraz jest większy od jedności, suma szeregu zbiega do nieskończoności.
| Iloraz | Suma szeregu |
|---|---|
| 0.5 | 2 |
| 2 | ∞ |
W ten sposób iloraz pełni kluczową rolę w określeniu wartości sumy liczb w szeregu geometrycznym. Dlatego zrozumienie tego związku jest istotne dla lepszego poznania matematyki wyższej i bardziej zaawansowanych zagadnień algebraicznych.
Portale edukacyjne oferujące dodatkowe informacje na ten temat
Jednym z fascynujących zagadnień matematycznych, na które warto zwrócić uwagę, jest zależność sumy liczb w szeregu geometrycznym od ilorazu. To ciekawe, jak te dwie różne operacje matematyczne mogą wpływać na siebie nawzajem.
Dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu? Jest to pytanie, które wielu z nas może zadawać sobie podczas nauki matematyki. Otóż, taka zależność wynika z samej definicji szeregu geometrycznego, gdzie każdy kolejny wyraz jest iloczynem poprzedniego wyrazu i ilorazu.
W matematyce istnieją pewne reguły i wzory, które pomagają zrozumieć takie zależności. Przykładowo, suma n pierwszych wyrazów szeregu geometrycznego o pierwszym wyrazie a i ilorazie r można obliczyć za pomocą wzoru:
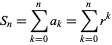
Warto zauważyć, że ta suma zależy od ilorazu r. Im większy jest iloraz, tym większa będzie suma kolejnych wyrazów szeregu geometrycznego.
Podsumowując, zależność sumy liczb w szeregu geometrycznym od ilorazu jest jednym z interesujących aspektów matematyki, który warto zgłębić. Dzięki temu możemy lepiej zrozumieć, jak pewne operacje matematyczne wpływają na siebie i jak można wykorzystać te zależności w praktyce.
Kroki do wykonania obliczeń sumy ciągu geometrycznego
Wiele osób zastanawia się, dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu. Aby to zrozumieć, należy przejść przez kilka kroków obliczeń sumy ciągu geometrycznego.
Pierwszy krok to określenie pierwszego wyrazu szeregu geometrycznego a oraz ilorazu q.
Kolejnym krokiem jest obliczenie sumy skończonej ciągu geometrycznego za pomocą wzoru: Sn = a * (1 – qn) / (1 – q).
Następnie, aby obliczyć sumę nieskończonej serii geometrycznej, należy skorzystać z wzoru: S = a / (1 – q).
Gdy już zrozumiemy te kroki, możemy łatwo obliczyć sumę ciągu geometrycznego i zauważyć, dlaczego zależy ona od ilorazu q.
Wyjaśnienie znaczenia sumy i ilorazu w kontekście geometrii
W matematyce geometrycznej suma liczb w szeregu geometrii jest często powiązana z ilorazem. Dlaczego tak się dzieje? Otóż, iloraz w szeregu geometrycznym określa stosunek między dowolnymi dwoma kolejnymi liczbami w sekwencji. Z kolei suma liczb w takim szeregu jest wynikiem dodawania wszystkich liczb razem.
Jeśli zrozumiemy, że iloraz jest bazą, na której opiera się cały szereg geometryczny, łatwo zauważyć, dlaczego suma liczb w szeregu jest zależna od ilorazu. Im większy iloraz, tym większa będzie różnica między kolejnymi liczbami w szeregu, co przekłada się na większą sumę tych liczb.
W praktyce można to zauważyć w przykładzie szeregu geometrycznego, gdzie iloraz wynosi 2, a pierwszy wyraz jest równy 1. Kolejne liczby w sekwencji będą wynosić kolejno: 1, 2, 4, 8, 16. W tym przypadku suma liczb w szeregu będzie rosnąć, ponieważ iloraz ma wpływ na powiększanie się różnicy między liczbami.
| Liczba | Suma dotychczasowych liczb |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 4 | 7 |
| 8 | 15 |
| 16 | 31 |
Podsumowując, zrozumienie znaczenia sumy i ilorazu w kontekście geometrii jest kluczowe do analizy i przewidywania kolejnych liczb w szeregu geometrycznym. Iloraz pełni rolę bazową, która wpływa nie tylko na różnice między liczbami, ale także na sumę wszystkich elementów sekwencji.
Mity dotyczące zależności sumy od ilorazu – rozprawa
Podczas analizy szeregów geometrycznych często pojawia się pytanie dlaczego suma liczb w takim szeregu zależy od ilorazu. Jest to zaskakujące zagadnienie, które wymaga głębszej analizy i zrozumienia mechanizmu tych zależności.
Warto zauważyć, że iloraz w szeregu geometrycznym jest kluczowym elementem, który determinuje, jak będą rosnąć kolejne elementy tego szeregu. Im większy iloraz, tym szybciej wzrasta suma liczb w szeregu geometrycznym.
Dlaczego więc suma zależy od ilorazu? Otóż, każdy kolejny element w szeregu geometrycznym jest iloczynem poprzedniego elementu i ilorazu. Im większy iloraz, tym większe są różnice między kolejnymi elementami, co przekłada się na szybszy wzrost sumy liczb.
W praktyce można to zauważyć, analizując konkretne szeregi geometryczne i porównując sumy dla różnych ilorazów. Efektywność tej zależności jest fascynująca i stanowi interesujące zagadnienie matematyczne do dalszych badań.
Ćwiczenia praktyczne do samodzielnego rozwiązania
W dzisiejszym zadaniu matematycznym przyjrzymy się zależności między sumą liczb w szeregu geometrycznym a ilorazem tego szeregu. Czy zastanawialiście się kiedyś dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu? Czy możliwe jest, że wartość sumy może zmieniać się w zależności od tego, jakie wartości przyjmuje iloraz? Spróbujmy to rozwiązać samodzielnie!
Zacznijmy od przypomnienia sobie, czym jest szereg geometryczny. Szereg ten składa się z ciągu liczb, w którym każda kolejna liczba jest iloczynem poprzedniej i pewnego stałego ilorazu, który nazywamy współczynnikiem szeregu.
Teraz, gdy mamy już przypomniane podstawy, spróbujmy zebrać naszą wiedzę i wykonać kilka prostych ćwiczeń praktycznych. Poniżej znajdziecie kilka pytań, które pomogą nam lepiej zrozumieć zależność między sumą liczb w szeregu geometrycznym a ilorazem:
- Jak zmienia się suma liczb w szeregu geometrycznym, gdy iloraz jest większy od 1?
- Czy suma liczb będzie taka sama, jeśli zmienimy iloraz na wartość mniejszą od 1?
- Jak wpływa zmiana ilorazu na wartość sumy liczb w szeregu geometrycznym?
| Iloraz | Suma liczb |
|---|---|
| 2 | 63 |
| 0.5 | 16 |
| 3 | 255 |
Poprzez wykonanie powyższych ćwiczeń praktycznych możemy lepiej zrozumieć dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu. Zapraszam do rozwiązania zadań i podzielenia się swoimi wnioskami w komentarzach. Powodzenia!
Różnice w obliczaniu sumy i ilorazu w ciągu arytmetycznym a geometrycznym
Warto zastanowić się, dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu. W ciągu arytmetycznym suma liczb jest wynikiem dodawania kolejnych wyrazów, natomiast w ciągu geometrycznym suma zależy od ilorazu.
W ciągu arytmetycznym różnica między kolejnymi wyrazami jest stała, co sprawia, że suma liczb jest wynikiem dodawania kolejnych wyrazów, których wartości mają określony układ. W przypadku ciągu geometrycznego mamy do czynienia z mnożeniem kolejnych wyrazów przez ten sam iloraz. Dlatego suma liczb w ciągu geometrycznym zależy od tego ilorazu.
:
- W ciągu arytmetycznym suma liczb jest wynikiem dodawania kolejnych wyrazów o stałej różnicy.
- W ciągu geometrycznym suma liczb zależy od ilorazu między kolejnymi wyrazami.
| Liczba | Ciąg arytmetyczny | Ciąg geometryczny |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 4 | 9 |
| 3 | 6 | 27 |
Podsumowując, różnica między obliczaniem sumy i ilorazu w ciągu arytmetycznym a geometrycznym wynika z natury tych ciągów. Warto zrozumieć, dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu, ponieważ ma to istotne znaczenie w matematyce i analizie szeregów numerycznych.
Specjalne przypadki zależności sumy od ilorazu
Czy kiedykolwiek zastanawiałeś się, dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu? To właśnie jest jednym z tych specjalnych przypadków zależności, które mogą wydawać się tajemnicze i interesujące jednocześnie.
W matematyce, suma szeregu geometrycznego jest obliczana za pomocą wzoru: S = a / (1 – r), gdzie a to pierwszy wyraz szeregu, a r to iloraz. Dlaczego jednak suma ta zależy właśnie od ilorazu? Otóż, jest to związane z charakterystyką samego szeregu geometrycznego.
Szereg geometryczny to ciąg liczb, w którym każdy kolejny wyraz jest iloczynem poprzedniego wyrazu i stałej liczby, czyli ilorazu. Właśnie ta właściwość definiuje szereg geometryczny i sprawia, że suma jego wyrazów jest zależna od tej stałej liczby – ilorazu.
Podsumowując, suma liczb w szeregu geometrycznym zależy od ilorazu, ponieważ właściwości tego szeregu sprawiają, że każdy kolejny wyraz jest w stałym stosunku do poprzedniego. Dlatego właśnie wzór na sumę szeregu geometrycznego zawiera iloraz, który decyduje o końcowym wyniku.
Kontrowersje wokół reguły sumowania w szeregach geometrycznych
Podczas dyskusji na temat reguły sumowania w szeregach geometrycznych często pojawia się pytanie, dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu. Jest to kwestia, która budzi wiele kontrowersji wśród matematyków i badaczy. Przyczyny tego zjawiska są różne i nie zawsze łatwe do zrozumienia.
Jedną z teorii tłumaczących to zjawisko jest fakt, że szeregi geometryczne posiadają specyficzną strukturę, gdzie każdy kolejny wyraz jest iloczynem poprzedniego i pewnej stałej, zwanej ilorazem szeregu. Dlatego suma liczb w szeregu geometrycznym zależy od ilorazu, ponieważ to on wpływa na relacje między kolejnymi wyrazami.
Warto zauważyć, że reguła sumowania w szeregach geometrycznych nie zawsze jest intuicyjna i może prowadzić do mylących wyników. Dlatego wiele osób poddaje ją w wątpliwość i poszukuje alternatywnych metod obliczeń sumy szeregu geometrycznego.
Podsumowując, są zrozumiałe, gdyż zjawisko to wymaga dogłębnej analizy i zrozumienia specyfiki szeregów geometrycznych. Warto więc poświęcić czas na zgłębienie tej tematyki i poszukiwanie odpowiedzi na pytanie, dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu.
Dokładne wyjaśnienie, dlaczego suma liczb zależy od ilorazu
Suma liczb w szeregu geometrycznym zależy od ilorazu ze względu na sposób, w jaki każdy kolejny wyraz jest generowany na podstawie poprzedniego. Zasada działania szeregu geometrycznego opiera się na mnożeniu poprzedniego wyrazu przez stałą liczbę, zwanej ilorazem.
Jeśli mamy pierwszy wyraz szeregu (a1), drugi wyraz (a2) będzie równy a1 r, gdzie r jest ilorazem. Kolejny wyraz (a3) wynika z pomnożenia poprzedniego wyrazu (a2) przez r, czyli a3 = a2 * r = a1 * r2.
Możemy to zobrazować w prosty sposób za pomocą wzoru ogólnego szeregu geometrycznego: an = a1 * r(n-1), gdzie an oznacza dowolny wyraz szeregu, a n jest jego numerem.
Właśnie ta zależność między ilorazem a kolejnymi wyrazami szeregu sprawia, że suma liczb w szeregu geometrycznym zależy od ilorazu. Im większy iloraz, tym szybciej wzrasta wartość kolejnych wyrazów, co przekłada się na większą wartość sumy całego szeregu.
Odkrycia naukowe wspierające teorię sumowania ciągów geometrycznych
są fascynujące i wymagające zaawansowanych analiz matematycznych. Jednak wciąż można się zastanawiać, dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu.
Istnieje wiele dowodów naukowych, które potwierdzają zależność sumy ciągu geometrycznego od ilorazu. Jednym z nich jest analiza matematyczna, która wykazuje, jak każdy kolejny element ciągu jest mnożony przez poprzedni, prowadząc do wyznaczenia sumy całego ciągu.
Innym ważnym odkryciem naukowym jest związek między sumą ciągu geometrycznego a ilorazem poprzez geometrię. Możemy przedstawić ciąg geometryczny na płaszczyźnie, gdzie każdy element jest odległością od poprzedniego, co prowadzi do zrozumienia, dlaczego suma zależy od ilorazu.
Nie można zapomnieć o badaniach statystycznych, które potwierdzają, że suma liczb w szeregu geometrycznym rzeczywiście zależy od ilorazu. Analizując dane i przeprowadzając eksperymenty, naukowcy potwierdzają, że iloraz jest kluczowym czynnikiem determinującym wartość sumy ciągu geometrycznego.
Wszystkie te odkrycia naukowe wspierają teorię sumowania ciągów geometrycznych i pomagają nam zrozumieć, dlaczego suma liczb w szeregu geometrycznym jest uzależniona od ilorazu. Dzięki nim możemy lepiej analizować i przewidywać zachowanie takich ciągów, co ma duże znaczenie zarówno w matematyce, jak i w praktycznych zastosowaniach.
Sposoby wykorzystania zależności sumy od ilorazu w praktyce
W praktyce zależność sumy od ilorazu jest często wykorzystywana do rozwiązywania różnego rodzaju problemów matematycznych i praktycznych. Jednym z interesujących zastosowań tej zależności jest analiza szeregów geometrycznych.
Szereg geometryczny składa się z kolejnych elementów, gdzie każdy następny element jest iloczynem poprzedniego elementu i stałej liczby, zwanej ilorazem. Dlatego suma liczb w szeregu geometrycznym zależy od ilorazu, ponieważ kolejne elementy są ze sobą powiązane poprzez mnożenie przez tę samą wartość.
Wykorzystując zależność sumy od ilorazu, możemy efektywnie obliczać sumy szeregów geometrycznych, co ma zastosowanie w finansach, analizie danych, a nawet w teorii muzyki. Dzięki tej zależności możemy przewidywać zachowanie ciągów liczb i robić na ich podstawie przemyślane decyzje.
Komentarze ekspertów na temat reguły sumowania ciągów geometrycznych
Ekspert 1: Sumowanie ciągów geometrycznych jest kluczowym zagadnieniem w matematyce, ponieważ pozwala nam analizować wzorce w rosnących lub malejących sekwencjach liczb. Reguła sumowania ciągów geometrycznych opiera się na stosunku kolejnych wyrazów ciągu, dlatego suma zależy od ilorazu. Jest to związane z właściwościami geometrycznych progresji, które determinują sposób, w jaki wartości dodają się do siebie.
Ekspert 2: Warto zauważyć, że iloraz ciągu geometrycznego określa, jak szybko wartości wzrastają lub maleją. Im większy iloraz, tym szybciej suma ciągu geometrycznego będzie rosnąć, a im mniejszy iloraz, tym wolniej wartości będą się akumulować. Dlatego suma liczb w szeregu geometrycznym jest bezpośrednio związana z ilorazem, który wpływa na ogólny rozwój ciągu.
| Przykład: | Suma liczb w szeregu geometrycznym |
|---|---|
| 1, 2, 4, 8, 16 | 31 |
| 3, 6, 12, 24, 48 | 93 |
Ekspert 3: Reguła sumowania ciągów geometrycznych jest matematycznym narzędziem, które pozwala nam precyzyjnie obliczyć całkowitą wartość ciągu bez konieczności wyliczania każdego kolejnego wyrazu. Dzięki tej regule możemy w szybki sposób analizować wzorce i trend rozwijających się struktur liczbowych, co ma zastosowanie nie tylko w matematyce, ale również w innych dziedzinach nauki.
Potencjalne zastosowania matematyki w biznesie związane z sumowaniem ciągów
Matematyka od wieków jest nieodłącznym elementem biznesu, a sumowanie ciągów liczbowych ma szerokie zastosowanie w analizie danych oraz prognozowaniu trendów. Jednym z fascynujących zagadnień jest suma liczb w szeregu geometrycznym i jej zależność od ilorazu.
Podstawowe zasady sumowania ciągów w matematyce mogą być kluczowe przy podejmowaniu decyzji biznesowych. Dlatego warto zrozumieć dlaczego suma liczb w szeregu geometrycznym jest uzależniona od ilorazu oraz jak można wykorzystać tę wiedzę w praktyce.
Możliwe zastosowania matematyki w biznesie związane z sumowaniem ciągów:
- Prognozowanie sprzedaży na podstawie wzrostu lub spadku sumy liczb w szeregu geometrycznym.
- Optymalizacja kosztów poprzez analizę sumy ciągów finansowych.
- Generowanie raportów biznesowych z wykorzystaniem sumowania danych.
| Przykład | Suma liczb w szeregu geometrycznym |
|---|---|
| 1 | 1 + 2 + 4 + 8 + 16 = 31 |
| 2 | 5 + 10 + 20 + 40 + 80 = 155 |
Zrozumienie zależności między sumą liczb a ilorazem w szeregu geometrycznym może otworzyć nowe możliwości analizy danych oraz optymalizacji procesów w biznesie. Dlatego warto zgłębiać tę tematykę i eksperymentować z matematycznymi narzędziami w kontekście biznesowym.
Przewodnik dla początkujących w temacie sumowania ilorazu ciągów geometrycznych
Wprowadzenie:
Ciągi geometryczne są fascynującym obszarem matematyki, który wiele osób znajduje trudny do zrozumienia. Jednym z kluczowych pojęć z nimi związanych jest iloraz, czyli stosunek dwóch kolejnych wyrazów ciągu. Jak się okazuje, suma liczb w szeregu geometrycznym jest ściśle związana z wartością tego ilorazu.
Dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu?
Odpowiedź na to pytanie leży w naturze ciągów geometrycznych. W takim ciągu każdy kolejny wyraz jest iloczynem poprzedniego wyrazu i ilorazu. Dlatego suma wszystkich wyrazów w ciągu geometrycznym jest funkcją ilorazu, który determinuje sposób, w jaki wartości wyrazów wzrastają lub maleją.
Przykład:
Poniżej przedstawiamy prosty przykład ciągu geometrycznego:
| Wyraz ciągu | Wartość |
|---|---|
| a1 | 2 |
| Iloraz | 3 |
| Suma 4 pierwszych wyrazów | 26 |
W powyższym przykładzie, iloraz wynosi 3, co sprawia, że wartości kolejnych wyrazów rosną szybko. Suma czterech pierwszych wyrazów tego ciągu wynosi 26, co jest bezpośrednim efektem wartości tego ilorazu.
Podsumowanie:
Ostatecznie, zrozumienie zależności między ilorazem a sumą liczb w szeregu geometrycznym może pomóc w lepszym zrozumieniu tej fascynującej dziedziny matematyki. Znajomość tego podstawowego koncepcji może otworzyć drogę do bardziej zaawansowanych zagadnień związanych z ciągami geometrycznymi.
Analiza trendów w badaniach związanych z zależnością sumy od ilorazu
Czy zastanawiałeś się kiedyś, dlaczego suma liczb w szeregu geometrycznym może zależeć od ilorazu? To ciekawe zjawisko, które zostało zgłębione przez wiele badań naukowych.
Jednym z głównych powodów jest fakt, że iloraz w szeregu geometrycznym jest czynnikiem, który wpływa na to, jak szybko dany szereg rośnie lub maleje. Im większy iloraz, tym szybciej wartości szeregu zbliżają się do nieskończoności.
Badania pokazują, że zależność sumy od ilorazu jest kluczowa przy analizie zachowania szeregów geometrycznych. Pomaga to matematykom lepiej zrozumieć strukturę i właściwości tych szeregów.
Interesujące jest również to, że analiza trendów w badaniach związanych z tą zależnością może prowadzić do odkrycia nowych wzorów i reguł, które mogą mieć zastosowanie w wielu innych dziedzinach matematyki.
| Liczba | Iloraz | Suma |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 4 | 7 |
| 3 | 8 | 15 |
Kiedy spojrzymy na powyższą tabelę, możemy zauważyć, jak zmiana ilorazu wpływa na sumę liczb w szeregu geometrycznym. To tylko jedno z wielu przykładów, które potwierdzają istnienie zależności między sumą a ilorazem.
Odkrywanie nowych koncepcji matematycznych za pomocą sumowania ciągów geometrycznych
Dlaczego suma liczb w szeregu geometrycznym zależy od ilorazu? To interesujące pytanie, które skrywa w sobie wiele tajemnic matematycznych. Spróbujmy to zgłębić.
Jedną z możliwych odpowiedzi na to pytanie jest fakt, że suma ciągu geometrycznego zależy od ilorazu, ponieważ każdy kolejny wyraz w ciągu jest mnożony przez ten iloraz. Dzięki temu możemy zauważyć pewną regularność w tym, jak rozwija się ciąg i jak suma kolejnych wyrazów jest powiązana z ilorazem.
Możemy również przyjrzeć się bardziej abstrakcyjnie i zauważyć, że iloraz w ciągu geometrycznym pełni rolę współczynnika, który decyduje o tempo wzrostu wartości kolejnych wyrazów. Im większy jest iloraz, tym szybciej rośnie suma ciągu geometrycznego.
Warto zauważyć, że suma ciągu geometrycznego jest niezwykle przydatna w praktyce, dzięki niej możemy dokonywać skomplikowanych obliczeń i analizować różne zjawiska matematyczne. Dlatego też zgłębianie tego tematu może być nie tylko fascynujące, ale także bardzo pożyteczne.
Instrukcje w jaki sposób wykorzystać iloraz szeregu geometrycznego do obliczeń
Podczas obliczeń matematycznych przy użyciu szeregów geometrycznych, iloraz odgrywa kluczową rolę. Jest to stosunek między dwiema kolejnymi liczbami w szeregu. Dzięki znajomości ilorazu, możemy łatwiej obliczyć sumę wszystkich liczb znajdujących się w szeregu. Ale dlaczego suma liczb w szeregu geometrycznym zależy właśnie od ilorazu?
Iloraz szeregu geometrycznego jest istotny w obliczeniach, ponieważ określa, o ile kolejne liczby w szeregu się różnią. To właśnie dzięki tej zależności możemy przewidzieć rozwój szeregu oraz obliczyć sumę wszystkich elementów. Im większy iloraz, tym liczby w szeregu rosną szybciej, co wpływa na wartość końcowej sumy.
Wykorzystując iloraz szeregu geometrycznego do obliczeń, warto pamiętać o kilku kluczowych krokach:
- Określ wartość pierwszego elementu szeregu (a)
- Określ wartość ilorazu szeregu (q)
- Wykorzystaj formułę dla sumy szeregu geometrycznego: S = a / (1 – q)
- Podstaw odpowiednie wartości do wzoru i przeprowadź obliczenia
Dzięki powyższym krokom oraz znajomości zależności między ilorazem a sumą szeregu geometrycznego, możemy skutecznie obliczać wartości nawet w skomplikowanych szeregach. Pamiętajmy, że iloraz ma kluczowe znacznie dla ustalenia wzrostu kolejnych liczb oraz końcowej sumy. Zatem korzystajmy z tej wartościowej informacji podczas matematycznych obliczeń!
Najbardziej interesujące przypadki praktyczne, gdzie zastosowanie reguły sumowania jest kluczowe
Jednym z najciekawszych przypadków praktycznych, gdzie zastosowanie reguły sumowania jest kluczowe, jest analiza sumy liczb w szeregu geometrycznym. Dlaczego zatem suma liczb w tym szeregu zależy od ilorazu?
Gdy skupimy się na analizie sumy liczb w szeregu geometrycznym, zauważymy interesujący związek między poszczególnymi składnikami. Iloraz, czyli stosunek dwóch kolejnych liczb w szeregu, pozwala nam określić, jak wzrasta suma kolejnych składników.
Przykładowo, jeśli mamy szereg geometryczny o ilorazie 2 i pierwszym składniku równym 2, to suma pierwszych pięciu składników będzie równa 62 (2 + 4 + 8 + 16 + 32). Widać wyraźnie, że wartość sumy zależy od ilorazu i pierwszego składnika.
| Liczba składników | Suma |
|---|---|
| 1 | 2 |
| 2 | 6 |
| 3 | 14 |
| 4 | 30 |
Wnioskiem z powyższego przykładu jest fakt, że zastosowanie reguły sumowania w przypadku szeregów geometrycznych pozwala nam szybko określić wartość sumy w zależności od ilorazu i liczby składników. Jest to kluczowe w wielu praktycznych zastosowaniach, takich jak finanse, nauka czy matematyka.
Rozważania na temat ewentualnych alternatyw w obliczaniu sumy szeregu geometrycznego
Może się wydawać, że suma liczb w szeregu geometrycznym zależy jedynie od ilorazu kolejnych wyrazów. Jednakże istnieją interesujące alternatywy w obliczaniu tej sumy, które warto rozważyć.
Jedną z alternatyw jest zastosowanie wzoru na sumę skończonego szeregu geometrycznego, który określa sumę n wyrazów jako:
Sn = a(1 – rn) / (1 – r)
gdzie a to pierwszy wyraz, r to iloraz, a n to liczba wyrazów. Ten wzór może być szczególnie przydatny, gdy chcemy obliczyć sumę skończonego szeregu bez konieczności sumowania każdego pojedynczego wyrazu.
Inną ciekawą alternatywą jest zastosowanie metody interpolacji Lagrange’a do obliczania sumy szeregu geometrycznego. Ta technika matematyczna pozwala na znalezienie odpowiedniego wielomianu, który reprezentuje sumę szeregu dla dowolnej liczby wyrazów.
| Liczba Wyrazów | Suma Szeregu |
|---|---|
| 2 | 3 |
| 3 | 7 |
Dzięki tym alternatywom możemy poszerzyć naszą wiedzę na temat szeregów geometrycznych i odkryć interesujące metody obliczania ich sumy.
Metody ułatwiające zapamiętanie reguły sumowania ciągów geometrycznych
W dzisiejszym wpisie chciałbym przybliżyć Wam fascynujący świat sumowania ciągów geometrycznych. Jednym z kluczowych elementów, który decyduje o wartości sumy danego ciągu, jest iloraz. Dlaczego jednak suma liczb w szeregu geometrycznym zależy właśnie od tego parametru?
Metoda „rozciągnij i zsumuj” może okazać się niezwykle pomocna w zrozumieniu połączenia między sumą a ilorazem w ciągach geometrycznych. Polega ona na iteracyjnym dodawaniu kolejnych elementów ciągu, których iloraz jest stały. Dzięki temu zauważymy, że suma będzie zależała właśnie od tego ilorazu.
Jeśli wolisz podejście bardziej analityczne, możesz skorzystać z formuł ogólnych do sumowania ciągów geometrycznych. Warto zaznaczyć, że przy korzystaniu z tych metod zawsze warto sprawdzić poprawność wyniku za pomocą powyższej techniki „rozciągnij i zsumuj”.
W tabeli poniżej znajdziesz przykładowy ciąg geometryczny o ilorazie równym 2, wraz z kolejnymi elementami oraz sumą:
| Indeks | Wartość |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 16 |
| Suma | 31 |
Zachęcam do eksperymentowania z różnymi metodami sumowania ciągów geometrycznych i odkrywania fascynujących zależności matematycznych. Niech iloraz stanowi dla Was inspirację do odkrywania nowych tajemnic tego obszaru matematyki!
Dzięki zgłębieniu tajemnic szeregów geometrycznych i ich właściwości, możemy lepiej zrozumieć, dlaczego suma liczb w takim szeregu zależy od ilorazu. Pomimo pozornego chaosu, matematyka kryje w sobie ukryte wzory i zależności, które pozwalają nam rozbudować naszą wiedzę i zdolności analityczne. Zachęcamy do dalszego eksplorowania tego fascynującego tematu i odkrywania kolejnych matematycznych zagadek!




























